머신 러닝의 목표는 데이터에서 여러 형태의 패턴을 발견하고 이 패턴을 이용해 무언가를 예측하는 것입니다. 이 기사를 통해서 여러분은 머신 러닝의 문제와 해법에 대한 논의의 틀을 얻게 될 것입니다.
이 기사의 첫 부분은 머신 러닝에 대한 정의와 응용 사례에 대한 소개로 시작합니다. 그 다음, 머신 러닝의 추상화에 대해 논하고, 이를 이용해 데이터, 모델, 최적화 모델, 최적화 알고리즘에 대한 논의의 틀을 세웁니다. 이 기사의 후반부에서는 모든 머신 러닝 방법론에 내재해 있는 근본적인 주제에 대해 논하고 머신 러닝을 사용하는 실전적인 안내로 마무리합니다. 그러면 마침내 여러분이 머신 러닝 연구와 연습을 진척시키는 방법을 이해하게 될 것입니다.
자, 그럼 시작해봅시다.
도대체 머신 러닝이란 무엇인가
머신 러닝은 일반적으로 데이터에서 여러 형태의 패턴을 발견하는 일련의 기술을 의미합니다. 자율주행 자동차에서부터 개인화된 인공지능 도우미에 이르기까지, 프랑스어와 대만어 사이의 번역에서부터 음성과 문자 사이의 번역까지 다양한 범주의 적용 사례가 있습니다. 이미 여러분의 일상에서 사용하고 있거나 잠재적으로 적용될 몇 가지 애플리케이션이 있습니다.
1. 이상 현상 감지 Detecting anomalies
웹사이트 트래픽의 급증 현상 인지 또는 비정상적 은행 거래 부각
2. 유사 내용 추천 Recommend similar content
검색 중인 상품 발견 또는 연관된 스매싱 매거진Smashing Magazine 기사 찾기
3. 미래 예측 Predict the future
인접한 차들의 경로 설계 또는 주식 시장에서의 추세 예측
이것들은 머신 러닝의 많은 응용 사례 중 몇 가지인데, 대부분의 응용 사례는 데이터에 내재된 분포를 배우는 것과 연관되어 있습니다. 분포는 이벤트와 각 이벤트의 확률을 명시합니다. 다음 예제를 봅시다.
- 50%의 확률로 아이템을 5달러 이하로 구매한다.
- 25%의 확률로 아이템을 5~10달러 가격으로 구매한다.
- 24%의 확률로 아이템을 10~100달러 가격으로 구매한다.
- 1%의 확률로 아이템을 100달러 초과 가격으로 구매한다.
이 분포를 이용하여 우리는 앞에서 언급한 과제 모두를 완수할 수 있습니다.
- 이상 현상 감지
100달러 구매가 일어나면, 이를 이상 현상이라고 자신 있게 말한다. - 유사 내용 추천
3달러의 구매가 발생하면 ‘아이템 5달러 이하로 구매’를 추천한다. - 미래 예측
어떤 사전 정보가 없다면 다음 구매는 5달러 이하로 예측할 수 있다.
데이터 분포를 연구하여 수많은 과제를 완수할 수 있습니다. 요약하면 머신 러닝의 목표 중 하나는 이 분포를 연구하는 것입니다.
좀 더 실제적인 표현을 하자면, 우리 목표는 특정한 입력값과 출력값을 갖는 특정 함수를 학습하는 것입니다. 우리는 이 함수를 모델model이라 부릅니다. 입력을 x라 합시다. 그러면 모델은 입력값 x를 받아서 다음과 같이 표시합니다.
f(x) = ax
여기에서 a는 모델의 매개변수입니다. 매개변수가 다르면 모델이 다른 사례가 됩니다. 다른 말로 표현하면 a=2인 모델은 a=3인 모델과 다릅니다. 머신 러닝에서 우리의 목표는 이 매개변수를 연구해 ‘좋은’ 결과를 얻을 때까지 이 값을 변경하는 것입니다. 어떤 a 값이 ‘좋은’ 결과를 내는지 어떻게 결정할 수 있을까요?
각 매개변수 a의 변화에 따라, 모델을 평가하는 방법을 정의합니다. 우선 f(x)의 출력값이 우리의 예측입니다. 그리고 y는 정답(label)으로, 참이며 희망하는 출력값입니다. 예측값과 정답으로 손실 함수를 정의할 수 있습니다. 손실 함수는 단순히 예측값과 정답의 차이인 |f(x) -y|가 되겠습니다. 이 손실 함수를 이용해 모델에 대해 다른 매개변수로 측정할 수 있습니다. 가능한 매개변수가 몇 개 있다면 각각 그 값을 대입해 손실 함수 값이 가장 작은 것을 선택하십시오!
하지만 대부분의 문제가 그렇게 간단하지 않습니다. 매개변수가 무한하면 어떻게 될까요? 0과 1 사이의 모든 소수라면 어떨까요? 0과 무한대 사이라면? 이로 인해 다음 주제인 머신 러닝에서의 추상화가 등장합니다. 우리는 머신 러닝의 다른 측면을 논하여 여러분의 지식을 데이터, 모델, 목표objective, 목표를 푸는 방법으로 세분화하고자 합니다. 정답이 매개변수를 구하는 수준을 초월하는, 수많은 도전 과제가 있습니다. 우리는 로봇을 제어하는 것과 같이 복잡한 문제를 어떻게 해결해낼까요? 자율주행 자동차를 어떻게 제어할까요? 얼굴을 인식하는 모델을 학습하는 것은 무엇을 의미할까요? 다음 섹션은 이러한 질문에 대한 답변을 얻는 데 도움을 줄 것입니다.
추상화
머신 러닝에는 다양한 수준의 특이성이 많은 주제들이 있습니다. 큰 그림 속에서 각각의 조각들이 어디에 자리하는지 더 잘 이해할 수 있도록 머신 러닝에서의 추상화를 알아봅시다. 이러한 추상화abstractions 는 머신 러닝을 주제별로 분류하여 여러분이 그 주제에 대해 이해하는 것을 쉽게 해줍니다. 다음 분류는 UC버클리대학의 조너선 쇼축Jonathan Shewchuck 교수의 방법을 따른 것입니다.
1.애플리케이션과 데이터 Application and Data
문제에 대한 가능한 입력값과 원하는 출력값을 생각해봅시다.
질문: 목표가 무엇인가? 데이터는 어떻게 구조화돼 있나? 정답이 제공되는가? 제공되는 입력값으로부터 출력값을 추출하는 것이 합리적인가?
예제: 목표는 손글씨로 쓴 숫자 그림을 분류하는 것이다. 입력값은 손글씨 숫자 이미지다. 출력값은 숫자다.
2. 모델 Model
고려하는 함수의 형태를 결정하라.
질문: 선형 함수로 충분한가? 2차 함수? 다항식? 어떤 형태의 패턴에 관심이 있나? 신경망은 적절한가? 로지스틱 회귀Logistic regression?
예제: 선형 회귀Linear regression
3. 최적화 문제 Optimization Problem
구체적인 목표를 수학의 공식으로 표현하라.
질문: 손실을 어떻게 정의하나? 성공은 어떻게 정의하나? 알고리즘에 편향을 반영하기 위해서 가중치를 추가 적용해야 하나? 우리의 목표 달성에 고려해야 하는 데이터의 불균형이 존재하나?
예제: |Ax-b|^2를 최소화하는 ‘x’를 구하라.
4. 최적화 알고리즘 Optimization Algorithm
최적화 문제를 푸는 방법을 결정하라.
질문: 해답을 손으로 계산할 수 있나? 반복 알고리즘이 필요한가? 이 문제를 풀기가 더 쉬운 동등한 것으로 변환할 수 있고, 이것을 풀 수 있나?
예제: 함수의 미분을 구하라. 이를 0으로 설정하라. 최적의 매개변수를 구하라.
추상화 1: 데이터
실제로 데이터를 모으고, 처리하고, 패키지하는 것이 이 전쟁의 90%입니다. 이 데이터는 다수의 샘플로 이루어지는데 그 각각은 입력값을 처리한 결과입니다. 예를 들면, 입력값이 개의 이미지가 될 수 있습니다. 그 첫 샘플은 우리 집에서 기르는 버나드 마운틴 독과 차우차우 교배종인 맥시Maxie의 사진입니다. 두 번째 샘플은 어린 코기인 찰리Charlie의 사진입니다.
모델을 학습시키는 과정에서, 데이터를 적절하게 다루는 것이 중요합니다. 적절히 다룬다는 것은 데이터를 적절하게 분류해야 하고, 그중 일부는 너무 빨리 사용하지 않아야 한다는 것을 의미합니다. 일반적으로 데이터는 세 부분으로 나눕니다.
- 학습용 세트 Training set
이것은 모델을 학습하는 데이터 세트입니다. 모델은 이 데이터 세트를 수백 번 돌려 볼 수도 있습니다. - 유효성 검사 세트 Validation set
이것은 모델을 평가하는 데이터 세트로 정확도를 평가하고 이에 따라서 모델이나 방법론을 조정합니다. - 테스트 세트 Test set
이것은 맨 마지막에 한 번, 정확성을 평가하기 위해 측정하는 데이터 세트입니다. 테스트 세트를 학습이 충분히 되지 않은 상태에서 돌려보면 모델이 테스트 세트에 대해 과적합overfit 결과를 낼 수 있기 때문에 한 번만 실행합니다. 과적합의 개념에 대해서는 나중에 상세하게 다룰 것입니다.
추상화 2: 모델
머신 러닝 방법은 다음 두 가지로 나뉩니다.
지도 학습
지도 학습Supervised Learning에서 알고리즘은 정답을 알고 있는 데이터를 다룹니다. 여기서는 다음 두 부류의 문제를 다룹니다.
- 분류Classification
각 샘플이 k 개의 클래스 {C_1, C_2, ... C_k} 중에서 어디에 속하는지를 결정합니다. 예를 들면, “이 개는 무슨 품종인가?” 이 개는 {"코기", "버나드 마운틴 독", "차우차우"...} 중 하나입니다.
- 회귀Regression
값을 가지는 출력(때로는 확률이기도 합니다)을 결정합니다. 예를 들면, “이 환자가 신경모세포종(안구암)일 확률이 얼마인가?”
비지도 학습
비지도 학습Unsupervised Learning에서 알고리즘은 정답을 모르는 데이터를 다룹니다. 여기에서는 다음과 같은 부류의 문제를 다룹니다.
- 클러스터링Clustering
샘플들을k개의 그룹으로 분류합니다. 그 결과로 이뤄진 그룹에 대해 정답은 모릅니다. “어떤 DNA 순열이 가장 비슷한가?” - 차원 축소Dimensionality reduction
데이터에서 (선형으로 독립적인) “유일한” 특성의 개수를 줄이세요. “얼굴에서 공통적인 특성에는 무엇이 있나?”
추상화 3: 최적화 목표
최적화 목표optimization objectives와 알고리즘을 다루기 전에 예제가 필요합니다. 최소제곱법Least squares이 표준 예제입니다. 관심을 최소제곱법의 특정한 형태에 한정해 살펴보고자 합니다. 여러 개의 점에 적절한 선을 긋는 아주 쉬운 문제부터 시작해봅시다.
1차 함수를 상기해봅시다.
y = m * x + b
이와 같은 선이 있다고 가정합시다. 이것이 진짜 기초 모델입니다.

이제 이 선 주위로 표본이 되는 점들이 있다고 합시다.
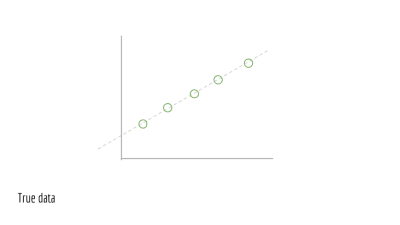
각 점에 대해 약간씩 위아래로 이동시킵니다. 다르게 표현하면 노이즈, 즉 무작위 섭동perturbation을 가합니다. 이 노이즈는 실세계에서 일어나는 현상의 반영입니다.

이것이 우리가 관찰하는 데이터입니다. 우리는 이 점들을 (x_1, y_1), (x_2, y_2), (x_3, y_3)··· 등으로 표현합니다. 이것은 학습 데이터로 모델 학습에 사용합니다. 이 데이터를 만든 숨어 있는 선(원래의 녹색 선)은 다루지 않습니다.

임의의 직선의 매개변수에 대해 알아봅시다. 이때 매개변수는 m과 b입니다. 이것으로 예측되는 선을 그리면 아래에 나타나는 파란 선입니다.

이 선이 얼마나 정확한지를 보기 위해서 파란 선을 측정해봅시다. m과 b를 이용해 y 값을 얻습니다. 우리는 일련의 ŷ 값들을 구합니다.
ŷ_i = m * x_i + b
예측 값 ŷ_i와 실제 값 y_i에 대한 오차는 간단하게 다음과 같습니다.
(ŷ_i−y_i)^2
전체 오차는 모든 샘플에 대한 위 값의 합입니다. 이것으로 손실은 다음과 같습니다.
∑(ŷ_i−y_i)^2
시각적으로 보면, 이것은 관찰된 점과 예측한 점 사이의 수직 거리를 가리킵니다.

위에서 ŷ_i 값에 대입해 m과 b의 항목으로 전체 오차를 구하면 다음과 같습니다.
∑(m * x_i + b − y_i)^2
궁극적으로 우리는 이 양을 최소화하려고 합니다. 이로부터 위의 추상화 3단계에서 구하는, 목표 함수objective function가 도출됩니다.
min_{m, b} ∑(m * x_i + b−y_i)^2
위 내용을 수학으로 표현하면, 목표는 m과 b의 값을 변화시키면서 손실을 최소화하는 것입니다. 이 섹션의 목적은 직선에 가장 일치하는 특별한 경우의 최소 제곱을 구하는 것입니다. 추가로 우리는 최소 제곱 목표least square objective를 계산으로 구했습니다. 다음은 이 목표에서 해를 구하는 것입니다.
추상화 4: 최적화 알고리즘
이것을 어떻게 최소화할까요? m에 대해 미분을 취하고, 0으로 설정한 다음 풉니다. 푼 결과로 분석적 해analytical solution를 얻습니다. 분석적 해를 구하는 과정이 최적화 알고리즘Optimization Algorithm으로 우리의 최적화 단계에서 네 번째이자 마지막 단계였습니다.
노트: 이 섹션의 중요한 부분은 여러분에게 최소제곱법이 닫힌 해closed form solution를 가진다는 점을 알려주기 위한 것입니다. 이 의미는 우리 문제의 최적 해법은 명시적으로 계산될 수 있다는 것입니다. 왜 이것이 중요한지를 이해하기 위해서, 닫힌 해가 없는 문제를 살펴보겠습니다. 예를 들어, 표준인 10단위의 로그 함수로 x=logx는 풀지 못합니다. 이 두 선을 그래프로 그려보면 이 두 선은 서로 만나지 않는다는 것을 알게 됩니다. 한편 일상의 최소제곱 방식은 닫힌 해를 갖는데 이것은 좋은 소식입니다. 최소제곱 방식으로 유도된 어떤 문제이든 우리는 주어진 데이터와 가설로부터 최적화 해를 계산할 수 있습니다.
근본적인 주제
더 많은 방법론을 공부하기 전에, 머신 러닝에 숨겨진 흐름를 이해할 필요가 있습니다. 이것들은 머신 러닝을 처음 공부하는 과정의 거의 전부라고 볼 수 있습니다.
편향-분산 거래 Bias-Variance Tradeoffs
머신 러닝에서 가장 염려하는 나쁜 사례의 하나가 과적합overfitting인데 이것은 모델이 학습 데이터에 너무 가까이 맞춰지는 경우에 일어납니다. 극단적으로 가장 과적합화한 모델은 데이터와 일치하는 경우일 것입니다. 만약 어떤 사람이 A 시험을 잘 치르면 이 사람은 B 시험에 대해서도 똑같은 준비를-시험 중간에 화장실에서 소변기를 사용했는지 여부까지-반복한다는 것을 의미합니다.
연관은 있지만 덜한 나쁜 사례는 과소적합underfitting인데 이것은 모델이 데이터에서의 중요한 정보를 잡아내지 못해 불충분하게 표현하는 것을 뜻합니다. 이것은 시험 성적을 예측하는 데 숙제 점수만 보고, 노트를 읽거나 실제 시험 결과 등은 무시하는 경우를 의미합니다. 우리의 목표는 일반적으로 적정한 구별을 해내는 결과를 도출하는 모델을 구축하는 것입니다.
이 두 가지 나쁜 사례에 대해 이들을 해소하기 위한 다양한 접근이 진행되고 있습니다. 하나는 최적화 목표를 수정해 모델의 복잡성에 벌점을 부과하는 개념을 포함하는 것입니다. 또 다른 경우는 목표나 알고리즘을 지배하는 하이퍼파라미터 hyperparameters 를 조정하는 것입니다. 이것은 ‘학습 속도’ 또는 ‘모멘텀’과 같은 개념으로 간주할 수 있습니다. 편향-분산 거래는 과적합과 과소적합을 정의하고 다루는 정밀한 방법을 우리에게 제공합니다.
최대우도추정Maximum Likehood Estimation, MLE + 최대사후확률Maximum A Posteriori, MAP
서로 다른 아이스크림 맛을 내는 A, B, C가 있다고 합시다. 우리에게는 서로 다른 레시피가 있습니다. 우리의 목표는 각각의 레시피가 어떤 맛을 내는지 예측하는 것입니다.
레시피에 기반해 맛을 예측하는 한 가지 방법은 다음 확률을 먼저 평가하는 것입니다.
P(flavor|recipe)
이 확률과 새로운 레시피가 주어지면 맛을 예측할 수 있을까요? 주어진 레시피에 대해 맛 A, B, C 각각의 확률을 단순하게 계산합니다.
P(flavor=A|recipe) = 0.4
P(flavor=B|recipe) = 0.5
P(flavor=C|recipe) = 0.1
그리고 가장 확률이 높은 것을 고릅니다. 위에서는 B가 주어진 레시피에서 가장 높은 확률입니다. 그러므로 우리는 B를 예측합니다. 수학적으로 위의 규칙을 다시 표현해보면 다음과 같습니다.
argmax_{flavor} P(flavor|recipe) # argmax means take the flavor that corresponds to the max value
그런데 우리의 처리 과정에서 유일한 정보는 그 반대인 주어진 맛에 대한 레시피의 확률입니다.
P(recipe|flavor)
최대우도추정 방법에 따르면 우리는 두 값이 비례한다는 가설을 세우고 찾습니다.
P(recipe|flavor) ~ P(flavor|recipe)
우리는 최대 확률 P(flavor|recipe)를 가지는 경우에만 관심이 있으므로 단순히 비례 값 P(recipe|flavor)에 대해 최대 확률인 경우만 찾습니다.
argmax_{flavor} P(recipe|flavor)
MLE는 위의 목표를 정답이 있는 데이터의 확률을 이용해 예측하는 한 가지 방법으로 제공합니다.
그런데 우리가 (x|y)를 가지고 있다는 가정을 하는 것이 합리적입니다. 우리는 관찰된 현실 데이터로부터 이것을 가늠해볼 수 있습니다. 예를 들어, 수업에 학생들이 가져오는 고무 오리의 숫자를 기반으로 학생들이 가져오는 구슬의 숫자를 예측해보고자 합니다.
데이터에서 각 학생들의 고무 오리 숫자는 x, 구슬의 숫자는 y로 표현합니다. 우리는 아래 데이터를 사용합니다.
| x | y |
|---|---|
| 1 | 2 |
| 1 | 1 |
| 1 | 2 |
| 2 | 1 |
| 2 | 2 |
| 1 | 2 |
P(x|y)가 주어졌다면 모든 y에 대해 x의 숫자를 계산할 수 있습니다. y=1인 모든 항목을 찾아봅시다. 두 개가 있는데 그중 하나는 x=1입니다. 그러므로 P(x=1|y=1) = 1⁄2이 됩니다. 모든 x, y값에 대해 이 작업을 반복합니다.
P(x=1|y=1) = 1/2
P(x=2|y=1) = 1/2
P(x=1|y=2) = 3/4
P(x=2|y=2) = 1/4
특징화, 정규화
최소제곱법으로 가장 적합한 선을 그립니다. 최소제곱법은 모델이 입력값 x와 출력값 y에서 선형이면 언제나 맞출 수 있습니다.
m=1이라 합시다. 그러면 다음 식을 얻습니다.
y = x + b
그런데 만약 우리의 데이터가 일반적인 선형이 아니면 어떻게 될까요? 특별히 샘플 데이터가 원형의 형태를 띠는 경우를 생각해봅시다. 원의 식은 다음과 같습니다.
x^2 + y^2 = r^2
최소제곱법이 이 경우에도 잘 맞을까요? 이 상태로는 아닙니다. 모델이 입력값 x와 출력값 y 에서 선형이 아닙니다. 대신 이 모델은 x와 y에서 2차 함수 형태를 가집니다. 그런데 약간 수정하면 여전히 최소제곱법을 사용할 수 있다는 것입니다. 이를 위해서 우리는 샘플 데이터에 특징을 가합니다.
다음을 생각해봅시다. 이 모델의 입력값이 x_ = x^2이고, y_ = y^2라면 어떻게 될까요? 그러면 우리 모델은 다음과 같은 모델을 학습하려고 시도하게 됩니다.
x_ + y_ = r^2
이 모델에서 입력 x_와 출력 y_는 선형인가요? 그렇습니다. 미묘한 부분이 있습니다. 현재 모델은 여전히 x, y에 대해 2차 함수이지만 x_, y_에 대해서는 선형입니다. 이것은 우리가 최소제곱을 학습하기 전에 x^2, y^2를 적용하면 최소제곱법을 이 데이터에 적용할 수 있다는 의미가 됩니다.
더 일반적으로 어떤 비선형 특징화featurization를 취해 특징이 비선형인 레이블에 최소제곱을 적용할 수 있습니다. 이것은 상당히 강력한 도구로 특징화라 불립니다.
그런데 특징화는 더욱 복잡한 모델이 됩니다. 정규화regularization는 모델의 복잡성에 벌점을 부과하게 하여 학습 데이터를 과적합하지 않도록 합니다.
결론
이 기사에서 우리는 머신 러닝의 근본적인 주요 주제들을 다루었습니다. 위에서 언급한 추상화를 이용해 머신 러닝의 문제와 해법을 다루는 프레임워크를 제공합니다. 위에서 다룬 근본적인 주제들을 이용해 이제 여러분은 머신 러닝 애플리케이션에서의 위험과 다른 우려 사항을 측정하는 데 필요한 도구를 제공하는 본질적인 개념에 대해 더 배울 수 있게 되었습니다.
더 읽어볼 만한 자료
우리는 계속해서 이 주제들–머신 러닝의 저변과 특정한 방법론-을 깊이 있게 다룰 것입니다. 그동안 여러분이 머신 러닝에 대해 추가 학습하고 연구할 만한 자료들을 제시합니다.
- “Introduction to Machine Learning,” Machine Learning course CS189, UC Berkeley
- NumPy(for efficient linear algebra utilities)
- scikit-learn(for out-of-the-box machine learning methods)

이단 마콧의 《반응형 디자인 패턴과 원리》
‘반응형 웹디자인’의 고안자, 이단 마콧의 《반응형 웹디자인》에서 한 걸음 더 나아간 책이다. 이 책에서는 반응형 내비게이션 시스템, 이미지 크기 조절과 배치, 반응형 맥락에서의 광고 관리, 기기에 종속되지 않는 가변적인 레이아웃을 디자인하기 위한 더 포괄적인 원리 등에 초점을 맞추어 성공적인 반응형 디자인 패턴과 원리를 제시한다.
books@webactually.com
